Xoilac TV xem bóng đá trực tuyến, trực tiếp bóng đá Xôi Lạc TV
Xoilac TV tự hào là kênh xem trực tiếp bóng đá với nội dung thể thao hấp dẫn số 1 Việt Nam. Tận hưởng trận đấu, bàn thắng đẹp và tin tức nhanh chóng cùng Xôi Lạc!
Link xem bóng đá Xoilac cập nhật ngày 18-04-2024
Xoilac TV là nền tảng xem trực tiếp bóng đá số 1, cùng với giao diện thân thiện, chất lượng hình ảnh sắc nét, Xoi Lac đem đến cho bạn những trận đấu hấp dẫn nhất từ khắp nơi trên thế giới. Thỏa mãn niềm đam mê bóng đá, tận hưởng không gian sống động, đậm chất fan hâm mộ tại địa chỉ uy tín này. Xem bóng đá không chỉ là giải trí, mà còn là niềm tự hào dành cho những người yêu thể thao.
Giới thiệu web xem trực tiếp bóng đá Xoilac
Xôi Lạc trực tiếp bóng đa hàng đầu
Xoilac tự tin là sân chơi bóng đá trực tuyến chất lượng hàng đầu. Với sứ mệnh mang đến niềm vui và kết nối cho cộng đồng yêu thể thao, Xoi lac cung cấp link trực tiếp bóng đá tuyệt vời và phát sóng TTBD đường truyền tốc độ cao không quảng cáo.
Giao diện thân thiện, tốc độ load nhanh, và chất lượng hình ảnh sắc nét là điểm mạnh của trang web. Từ các giải đấu quốc tế đến các trận đấu trong nước, nơi đây đem đến những khoảnh khắc căng thẳng và hồi hộp trực tiếp tại tầm tay bạn. Hãy đồng hành cùng Xoi lac và chia sẻ niềm đam mê bóng đá với hàng triệu người hâm mộ trên khắp thế giới.
Mục đích ra đời của kênh xem trực tiếp bóng đá Xoilac
Mục đích ra đời của web xem bóng đá Xôi Lạc
Xôi Lạc được tạo ra với mục tiêu mang đến trải nghiệm xem trực tiếp bóng đá chất lượng cao, giúp người hâm mộ thể thao thỏa mãn đam mê của họ và tận hưởng các trận đấu hấp dẫn nhất. Ngoài ra kênh Xoilac TV còn muốn tạo ra một cộng đồng trực tuyến cho những người yêu thích bóng đá, nơi người chơi có thể tương tác, trò chuyện và chia sẻ cảm xúc về các trận đấu.
Bên cạnh đó kênh muốn thúc đẩy sự phát triển của thị trường xem bong da trực tuyến, cung cấp một tùy chọn thú vị cho những người muốn theo dõi các trận đấu trực tiếp mà không cần đến sân vận động. Mục tiêu của Xôi Lạc là cung cấp thông tin thêm về các trận đấu, đội hình, thống kê, tin tức liên quan và nhiều nội dung khác, giúp người xem có cái nhìn toàn diện hơn về thế giới bóng đá.
Xoilac sứ mệnh phát triển nền tảng xem bóng đá trực tiếp chất lượng cao trong tương lai
Xôi Lạc tự tin xứ mệnh phát triển bóng đá trực tiếp trong tương lai
Phát triển nền tảng xem bóng đá trực tiếp chất lượng cao của Xoilac TV trong tương lai có thể bao gồm:
-
Xoi Lac hướng đến việc cung cấp chất lượng hình ảnh trực tiếp bóng đá vượt trội, đảm bảo mọi chi tiết trận đấu được truyền tải một cách rõ ràng và sắc nét, mang lại trải nghiệm hấp dẫn nhất cho người xem.
-
Kênh có thể tiếp tục đổi mới công nghệ để áp dụng các tính năng tiên tiến như tương tác thực tế ảo, trí tuệ nhân tạo, góc nhìn đa dạng và nhiều yếu tố khác để làm cho trải nghiệm xem bóng đá trở nên tươi mới và hấp dẫn hơn.
-
Xoi Lac cam kết tuân thủ các quy định về bản quyền và luật pháp liên quan đến việc phát sóng trực tiếp bóng đá, đảm bảo sự hợp pháp và bảo vệ quyền lợi của người tạo ra nội dung và các bên liên quan.
Mục tiêu phát triển của Website xem trực tiếp bóng đá Xoilac
Những mục tiêu phát triển của Xôi Lạc trong tương lai
Website xem trực tiếp bóng đá Xôi Lạc có những mục tiêu phát triển sau:
-
Xoi Lac hướng đến việc cải thiện liên tục giao diện người dùng, tối ưu hóa tốc độ tải trang và chất lượng hình ảnh để mang lại trải nghiệm tốt nhất cho người dùng.
-
Xem bóng đá trực tiếp tại kênh Xoi Lac TV quyết tâm cung cấp lịch trình đa dạng và rộng rãi hơn, từ các giải đấu quốc tế lớn đến các trận đấu cấp địa phương, để đáp ứng nhu cầu của đa dạng fan hâm mộ bóng đá.
-
Xôi Lạc tạo điều kiện cho cộng đồng người hâm mộ bóng đá kết nối và tương tác thông qua các tính năng xã hội, trò chuyện trực tuyến và phản hồi từ người dùng.
-
Kênh luôn theo dõi xu hướng công nghệ để áp dụng những cải tiến mới như tích hợp trí tuệ nhân tạo, giao diện thực tế ảo, hay khả năng tương tác đa phương tiện để làm cho trải nghiệm xem bóng đá trở nên thú vị và hiện đại hơn.
-
Xôi Lạc cam kết đảm bảo tính chính xác và đáng tin cậy của thông tin trận đấu, lịch thi đấu, và các dịch vụ liên quan đến bóng đá, để người dùng luôn cảm thấy tin tưởng khi sử dụng trang web.
-
Kênh trực tiếp bóng đá Xôi Lạc luôn hướng đến việc thu hút và phục vụ một lượng lớn người dùng mới, bao gồm cả những người không chỉ là fan bóng đá mà còn là những người tìm kiếm giải trí thể thao đa dạng.
Xoilac tự tin là kênh xem trực tiếp bóng đá được yêu thích nhất hiện nay
Kênh Xôi Lạc xem trực tiếp bóng đá chất lượng số 1 hiện nay
Xoi lac tự tin khẳng định vị trí dẫn đầu trong lĩnh vực live bóng đá và vượt qua các kênh trực tiếp bóng đá hiện nay như Socolive TV, với sự yêu thích không ngừng từ cộng đồng người hâm mộ. Chất lượng hình ảnh sắc nét, giao diện thân thiện và đa dạng lịch trình giải đấu là những yếu tố giúp Xôi Lạc trở thành điểm đến hàng đầu để thỏa mãn niềm đam mê bất tận của những người yêu bóng đá. Với sứ mệnh mang lại niềm vui và hạnh phúc thông qua trải nghiệm bóng đá tương tác, Xoi lac đang góp phần kết nối và lan tỏa đam mê thể thao trên khắp mọi miền đất nước và cả thế giới.
Tại sao kênh bóng đá trực tuyến tại Xoilac lại được yêu thích nhất hiện nay?
Các ưu điểm nổi bật của kênh bóng đá xem miễn phí Xoi Lac
Kênh bóng đá trực tiếp Xoi Lac có những ưu điểm nổi bật sau:
Chất lượng hình ảnh đỉnh cao
Xoi Lac cung cấp chất lượng hình ảnh sắc nét, đảm bảo người xem không bỏ lỡ bất kỳ chi tiết nào trong trận đấu. Với các thiết kế giao diện đơn giản, dễ sử dụng, giúp người dùng dễ dàng tìm kiếm và truy cập các trận đấu mong muốn.
Lịch trình đa dạng
Kênh xem bóng đá trực tiếp Xoilac cung cấp lịch trình đa dạng từ các giải đấu quốc tế đến các trận đấu địa phương, đáp ứng đa dạng nhu cầu của các fan hâm mộ. Xoi Lac tích hợp tính năng tương tác xã hội, cho phép người dùng thảo luận, trao đổi và chia sẻ cảm xúc với những người cùng đam mê.
Tích hợp thông tin chi tiết
Ngoài việc cung cấp trận đấu trực tiếp, Xoi Lac cũng cung cấp thông tin chi tiết về đội hình, thống kê, lịch sử thi đấu, kết quả, tin tức liên quan,... giúp người dùng có cái nhìn toàn diện về trận đấu. Xoi Lac cam kết cung cấp thông tin chính xác và đáng tin cậy về lịch thi đấu, kết quả và các thông tin liên quan đến bóng đá.
Khả năng tương thích
Xôi Lạc hỗ trợ trên nhiều thiết bị và nền tảng, cho phép người dùng xem trực tiếp bóng đá mọi lúc, mọi nơi. Kênh luôn tìm kiếm và tích hợp những cải tiến công nghệ mới, giúp cải thiện trải nghiệm xem bóng đá của người dùng.
Một số tính năng hot khác chỉ có tại Xoilac
Một số tính năng nổi bật khác của Xoi Lac
Ngoài việc cung cấp trải nghiệm xem trực tiếp bóng đá chất lượng cao, Xôi Lạc còn có thể tích hợp một số tính năng khác để tăng cường trải nghiệm của người xem. Dưới đây là một số ví dụ về các tính năng mà Xôi Lạc có thể cung cấp:
Xem tin tức bóng đá Xoilac
Xem tin tức bóng đá tại Xoi Lac không chỉ là cách để người hâm mộ cập nhật thông tin mới nhất về thế giới bóng đá, mà còn là cánh cửa mở ra với những chi tiết thú vị, câu chuyện đằng sau sân cỏ và những sự kiện xoay quanh môn thể thao vua. Từ những thông tin về đội bóng, cầu thủ, chuyển nhượng đến các bài phân tích chi tiết về các trận đấu, tin tức bóng đá mang đến một cái nhìn toàn diện và sâu sắc về một thế giới đang luôn sống động và thay đổi. Nó còn là nguồn cảm hứng, thúc đẩy niềm đam mê và kết nối người hâm mộ của Xôi Lạc lại với nhau thông qua việc trao đổi ý kiến và chia sẻ cảm xúc về những gì đang diễn ra trong giới bóng đá.
Xem lịch thi đấu bóng đá tại Xoilac
Xem lịch thi đấu bóng đá tại Xôi Lạc là một trải nghiệm thú vị và hữu ích cho người yêu thể thao. Trang web cung cấp cho bạn lịch thi đấu chi tiết của các giải đấu quốc tế và quốc gia, từ World Cup, Euro, Copa America đến các giải vô địch hàng đầu như Premier League, La Liga, Serie A và Bundesliga. Bạn có thể dễ dàng theo dõi ngày, giờ và địa điểm của các trận đấu, giúp bạn không bỏ lỡ bất kỳ trận cầu nào.
Xoilac cung cấp tính năng xem bảng xếp hạng bóng đá hấp dẫn
Tính năng "Xem bảng xếp hạng bóng đá" tại Xôi Lạc mang đến cho bạn một cái nhìn tổng quan về vị trí và hiệu suất của các đội bóng trong các giải đấu. Điều này giúp bạn dễ dàng theo dõi sự thay đổi trong thứ hạng và xác định được những đội mạnh, yếu đang thi đấu thế nào. Bảng xếp hạng được cập nhật thường xuyên, giúp bạn nắm bắt được tình hình thay đổi mới nhất trong các giải đấu.
Bạn có thể so sánh hiệu suất của các đội bóng và xem xét cách các cầu thủ đối đầu với nhau trong bảng xếp hạng Xoi lac. Dựa vào bảng xếp hạng, bạn có thể ước tính vị trí và cơ hội tiến xa của các đội trong giai đoạn kết thúc giải đấu. Tính năng này giúp bạn nhận biết được những đội bóng nào đang có khả năng tranh chức vô địch và những cuộc đua quyết liệt trên bảng xếp hạng.
Xem kết quả bóng đá ở Xoilac
Xem kết quả bóng đá tại Xoi Lac là một cách tiện lợi và nhanh chóng để cập nhật thông tin về các trận đấu. Bạn có thể dễ dàng tìm thấy kết quả của các trận đấu quốc tế và quốc gia, từ những giải đấu lớn cho đến các giải vô địch quốc gia hàng đầu và nhiều giải khác. Việc theo dõi kết quả bóng đá tại Xoi Lac giúp bạn nhanh chóng biết được kết quả của các trận đấu, bàn thắng được ghi, cũng như những sự kiện quan trọng trong mỗi trận. Điều này giúp bạn cảm nhận được nhịp đập và diễn biến của thế giới bóng đá một cách hiệu quả và thuận tiện.
Xem highlight bóng đá tại trang web Xoilac
Trang web xem truc tiep bong da Xoi lac cung cấp cho bạn những video tóm tắt về các trận đấu, giúp bạn nhanh chóng cập nhật các sự kiện quan trọng như bàn thắng, pha phối hợp nổi bật và những tình huống kịch tính. Bằng cách xem highlight bóng đá tại Xoi Lac, bạn có thể bắt kịp các diễn biến quan trọng trong thế giới bóng đá mà không cần phải xem toàn bộ trận đấu. Đây là một cách tiện lợi và thú vị để thỏa mãn niềm đam mê và cảm nhận tinh thần của môn thể thao vua một cách nhanh chóng và hiệu quả.
Xem tỷ lệ kèo trực tiếp bóng đá tại Xoilac TV
Xem tỷ lệ kèo bóng đá tại Xoi Lac là một cách để bạn có cái nhìn tổng quan về cơ hội chiến thắng trong các trận đấu. Tỷ lệ kèo thể hiện sự đánh giá về khả năng của các đội bóng trong trận đấu, được tính toán dựa trên nhiều yếu tố như sự thể hiện gần đây, thành tích đối đầu và điều kiện thể lực.
Xem nhận định trước trận đấu trên nền tảng Xoilac
Việc xem nhận định trước trận đấu ở kênh xem bóng đá trực tiếp Xôi Lạc giúp bạn có cái nhìn sâu rộ và chi tiết về trận đấu, từ đó có thể giúp bạn đưa ra quyết định cá cược thông minh hơn. Tuy nhiên, hãy nhớ rằng dự đoán bóng đá luôn mang tính chất không chắc chắn, và kết quả thực tế có thể khác với nhận định trước trận.
Lý do bạn nên xem trực tiếp bóng đá cực hấp dẫn tại Xoilac?
Lý do bạn nên xem trực tiếp bóng đá tại Xôi Lạc?
Có một số lý do mà bạn có thể thấy hấp dẫn khi xem bóng đá tại Xoi Lac:
Xem bóng đá trực tiếp hấp dẫn tại Xoilac với chất lượng cao
Coi đá banh Xoi lac với chất lượng cao tại Xôi Lạc là một trải nghiệm thú vị dành cho những người yêu thể thao. Với cam kết mang đến hình ảnh sắc nét và đỉnh cao, Xôi Lạc cho phép bạn theo dõi mỗi tình huống kịch tính trên sân cỏ một cách rõ ràng và chân thực. Không chỉ giới hạn trong việc truyền tải trận đấu, Xôi Lạc còn cung cấp thông tin đa dạng về đội hình, thống kê, tin tức và nhiều nội dung liên quan khác, giúp bạn hiểu rõ hơn về trận đấu và thế giới bóng đá.
Xem trực tiếp bóng đá miễn phí
Tại Xôi Lạc, quý khách hàng có thể tận hưởng niềm vui của việc xem TTBD Xoilac miễn phí. Với sự cam kết về trải nghiệm chất lượng cao, bạn sẽ được đắm chìm trong từng khoảnh khắc căng thẳng và hồi hộp trên sân cỏ mà không cần phải tốn kém.
Đội ngũ BLV, Hỗ trợ chuyên nghiệp
Đội ngũ BLV (Bình luận viên) và đội hỗ trợ chuyên nghiệp tại Xoi lac đóng vai trò quan trọng trong việc mang đến trải nghiệm xem bóng đá trực tiếp chất lượng cao và thú vị cho khán giả. Với kiến thức sâu rộ về bóng đá và kinh nghiệm đa dạng, các BLV tại Xôi Lạc không hề thua kém Socolive, BLV Xoilac TV không chỉ cung cấp các thông tin cơ bản về trận đấu, mà còn đưa ra những phân tích sâu sắc về chiến thuật, tình hình của các đội, và những điểm nhấn đáng chú ý.
Thưởng thức bóng đá mọi lúc mọi nơi
Không còn phải ràng buộc bởi thời gian và địa điểm, bạn có thể tận hưởng mỗi khoảnh khắc hấp dẫn trên sân cỏ bất kể bạn đang ở đâu. Trong giờ làm việc, trên đường đi, tại nhà hoặc bất cứ nơi nào có kết nối Internet, bạn đều có thể đắm chìm vào những trận đấu kịch tính và cảm nhận niềm hứng thú của bóng đá tại kênh xem bong da truc tiep tại Xôi Lạc. Tận dụng công nghệ để thưởng thức bóng đá mọi lúc mọi nơi không chỉ là một cách tuyệt vời để kết nối với thế giới thể thao, mà còn là cách thú vị để tận hưởng niềm đam mê và tạo ra những trải nghiệm thú vị trong cuộc sống hàng ngày.
Xoi Lac trực tiếp toàn bộ các giải bóng đá lớn
Xoi Lac đem đến cho bạn khả năng thưởng thức trực tiếp toàn bộ các giải bóng đá lớn, mang đến trải nghiệm tuyệt vời và không giới hạn cho người hâm mộ. Từ những trận đấu kịch tính trong các giải quốc tế như World Cup, Euro, Copa America đến những trận cầu đỉnh cao trong các giải vô địch quốc gia hàng đầu như Premier League, La Liga, Serie A, Bundesliga và nhiều giải đấu khác, Xoi lac đảm bảo bạn không bỏ lỡ bất kỳ trận đấu nào.
Xoilac nói không với quảng cáo
Xoi Lac hỗ trợ trực tiếp bóng đá mà không chèn quảng cáo giữa các trận đấu. Với cam kết đem đến trải nghiệm xem bóng đá tốt nhất cho người hâm mộ, Xoi Lac đảm bảo không làm phiền người xem bằng các quảng cáo không mong muốn hay gián đoạn trong quá trình thưởng thức trận đấu. Từ những giải bóng đá lớn đến các trận đấu địa phương, Xoi lac TV mang đến những trận cầu hấp dẫn và mãn nhãn, với chất lượng hình ảnh và âm thanh đỉnh cao. Hãy tận hưởng mỗi khoảnh khắc căng thẳng và hồi hộp của bóng đá mà không phải lo lắng về những quảng cáo không mong muốn.
Hệ thống link xem bóng đá trực tiếp mượt mà
Hệ thống link trực tiếp bóng đá Xoilactv được tối ưu hóa để đảm bảo sự mượt mà và ổn định, không khác gì việc xem phim Hollywood. Với tốc độ cao và chất lượng hình ảnh sắc nét, bạn sẽ tận hưởng trận đấu mà như đang ngồi trên khán đài sân cỏ. Xôi Lạc cam kết mang đến cho bạn trải nghiệm xem bóng đá chất lượng hàng đầu, vượt trội và không gặp phải sự gián đoạn trong suốt cuộc trận.
Các trận xem trực tiếp bóng đá siêu hot và cuốn hút tại Xoilac
Các trận bóng đá đỉnh cao, cuốn hút ở Xôi Lạc
Xôi Lạc cung cấp nhiều trận đấu bóng đá siêu hot và cuốn hút từ các giải đấu hàng đầu trên thế giới. Dưới đây là một số trận đấu đáng chú ý mà bạn có thể xem trực tiếp tại Xoilac:
Coi trực tiếp Ngoại Hạng Anh - Premier League tại Xoilac
Tại Xôi Lạc, bạn có thể xem trực tiếp các trận đấu hấp dẫn từ Ngoại Hạng Anh - Premier League, giải đấu bóng đá hàng đầu tại Anh. Xôi Lạc cung cấp một nền tảng trực tuyến thuận tiện và đáng tin cậy để bạn không bỏ lỡ bất kỳ trận đấu nào của các đội bóng hàng đầu như Manchester United, Manchester City, Liverpool, Chelsea, Arsenal và nhiều đội bóng khác.
Xem trực tiếp Tây Ban Nha – La Liga tại Xoilac
Với chất lượng cao và ổn định, bạn có thể theo dõi các trận đấu căng thẳng, những siêu sao tài ba như Messi, Ronaldo, hoặc các đội bóng hàng đầu như Real Madrid, Barcelona, Atletico Madrid trình diễn tuyệt phẩm trên sân cỏ Tây Ban Nha. Hãy cùng Xoi Lac tận hưởng không gian bóng đá đích thực và không bỏ lỡ bất kỳ trận đấu nào của La Liga!
Xem bóng đá trực tiếp Đức – Bundesliga tại Xoilac
Xem bóng đá Xoi lac trực tiếp Đức - Bundesliga tại Xôi Lạc mang đến cho người xem những khoảnh khắc đỉnh cao của bóng đá châu Âu. Với sự cạnh tranh khốc liệt và tài năng của các cầu thủ, Bundesliga luôn thu hút sự chú ý của các fan hâm mộ trên khắp thế giới. Tại Xôi Lạc, bạn có cơ hội xem các trận đấu kịch tính, các bàn thắng mãn nhãn và những pha bóng tài ba từ các đội bóng như Bayern Munich, Borussia Dortmund, và nhiều đội tên tuổi khác. Dừng lại và cùng Xôi Lạc đắm chìm trong không gian bóng đá Đức đẳng cấp!
Xem TTBD Ý – Serie A
Các trận đấu trong Serie A luôn đem lại những khoảnh khắc mãn nhãn, từ những bàn thắng đẹp mắt đến những pha bóng sáng tạo. Hãy tham gia vào Xôi Lạc để không chỉ thấy các đội bóng như Juventus, AC Milan, Inter Milan cạnh tranh với nhau một cách quyết liệt, mà còn cảm nhận được văn hóa bóng đá độc đáo của nước Ý qua những trận cầu nảy lửa và đầy cảm xúc.
Xem bóng đá trực tuyến cúp C1, C2 tại Xoilac TV
Xem trực tiếp cúp C1 (Champions League) và cúp C2 (Europa League) là một trải nghiệm không thể thiếu cho các người hâm mộ bóng đá. Tại Xôi Lạc TV, chúng tôi cung cấp cơ hội độc đáo để bạn theo dõi những trận cầu đỉnh cao của các đội bóng hàng đầu châu Âu. Bạn có thể tận hưởng những pha bóng mãn nhãn, những bàn thắng nghẹt thở và những tình huống kịch tính trên sân cỏ.
Xem TTBD V-League tại Xoilac TV
Xem trực tiếp V-League tại Xôi Lạc TV mang đến cho bạn cơ hội thưởng thức những trận đấu đầy kịch tính và hấp dẫn trong giải đấu hàng đầu của bóng đá Việt Nam. Tận hưởng những pha bóng nhanh, các tình huống ghi bàn và những bước tiến của các đội bóng trong hành trình chinh phục ngôi vị vô địch.
Các giải đấu bóng đá chất lượng đỉnh cao khác chỉ có tại Xoilac
Xôi Lạc không chỉ cung cấp xem trực tiếp bóng đá từ các giải đấu hàng đầu như Premier League, La Liga, Serie A, Bundesliga, Champions League và Europa League, mà còn liên tục cập nhật các giải đấu thể thao quan trọng khác trên khắp thế giới. Bạn có thể tận hưởng những trận đấu sôi động từ các giải đấu như:
-
V-League (Việt Nam)
-
Eredivisie (Hà Lan)
-
J-League (Nhật Bản)
-
MLS (Mỹ)
-
Các giải đấu quần vợt, đua xe F1, Olympic và nhiều giải thể thao quan trọng khác.
Hướng dẫn xem trực tiếp bóng đá tại Xoilac nhanh chóng và đơn giản
Các cách xem bóng đá trực tiếp Xôi Lạc nhanh chóng
Xoi Lac là một trang web cung cấp dịch vụ xem trực tiếp các trận đấu bóng đá và thể thao từ các giải đấu hàng đầu trên thế giới. Việc xem trực tiếp bóng đá tại Xôi Lạc rất dễ dàng và tiện lợi. Dưới đây là hướng dẫn cụ thể:
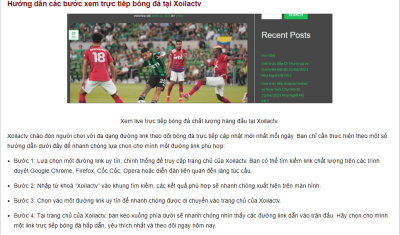
Bước 1: Truy cập Trang Web
Đầu tiên, mở trình duyệt web trên thiết bị của bạn và truy cập vào trang web của Xoilac. Bạn có thể tìm kiếm trang web này trên các công cụ tìm kiếm hoặc nhập trực tiếp địa chỉ vào thanh địa chỉ.
Bước 2: Tìm Lịch Thi Đấu
Trên trang chính của Xoi Lac, bạn sẽ thấy các thông tin về lịch thi đấu các trận bóng đá đang diễn ra hoặc sắp tới. Chọn trận đấu bạn muốn xem trực tiếp. Sau khi bạn chọn trận đấu, trang web sẽ hiển thị các kênh trực tiếp tương ứng với trận đấu đó. Bạn chỉ cần nhấp vào kênh mà bạn muốn xem.
Bước 3: Xem Trực Tiếp
Khi bạn chọn kênh trực tiếp, trang web sẽ mở ra một giao diện xem trực tiếp bóng đá. Bạn có thể thấy video trực tiếp, thông tin về trận đấu, và các tùy chọn điều chỉnh âm thanh và chất lượng. Bây giờ, bạn đã sẵn sàng tận hưởng trận đấu bóng đá trực tiếp trên Xôi Lạc. Bạn có thể thả mình vào không gian bóng đá hấp dẫn mà trang web này mang lại.
Cách tải app Xoilac nhanh chóng nhất hiện nay
Cách tải App Xoilac cực nhanh chóng cho người mới
-
Mở cửa hàng ứng dụng trên thiết bị di động của bạn (Google Play Store cho Android hoặc App Store cho iOS).
-
Sử dụng tính năng tìm kiếm trong cửa hàng ứng dụng để tìm kiếm "Xoilac". Sau đó, nhấn vào kết quả tìm kiếm liên quan đến ứng dụng.
-
Nhấn vào nút tải xuống (hoặc "Get" hoặc "Install") để tải và cài đặt ứng dụng Xôi Lạc lên thiết bị của bạn.
-
Sau khi tải xong, mở ứng dụng Xôi Lạc từ màn hình chính hoặc từ mục ứng dụng.
Khán giả hâm mộ nói gì về kênh xem trực tiếp bóng đá Xoilac
Các khán giả nói gì về kênh bóng đá hàng đầu Xôi Lạc
Khán giả hâm mộ rất đánh giá cao Xoi Lac là một kênh xem trực tiếp bóng đá đáng tin cậy. Người dùng khen ngợi về chất lượng hình ảnh sắc nét, tốc độ phát sóng ổn định và khả năng cập nhật lịch thi đấu đầy đủ. Các fan bóng đá thường bày tỏ sự hài lòng về việc có thể theo dõi các trận đấu yêu thích mọi lúc, mọi nơi thông qua Xôi Lạc. Nhờ vào khả năng cung cấp các trận đấu từ các giải đấu hàng đầu thế giới, Xôi Lạc đã tạo ra một cộng đồng người hâm mộ bóng đá đầy phấn khích và không ngừng phát triển.
Một số câu hỏi thường gặp về kênh trực tiếp bóng đá Xoilac
Một số câu hỏi thường gặp về Xoi Lac
Dưới đây là một số câu hỏi thường gặp (FAQ) về kênh trực tiếp bóng đá Xôi Lạc:
Làm thế nào để xem trực tiếp bóng đá trên Xoilac?
Bạn có thể truy cập trang web hoặc ứng dụng bóng đá trực tuyến Xoilac, tìm kiếm trận đấu bạn muốn xem, và nhấn vào liên kết trực tiếp để xem trận đấu.
Xoilac có miễn phí hay phải trả tiền để sử dụng?
Thường thì Xôi Lạc cung cấp dịch vụ xem trực tiếp bóng đá miễn phí cho người dùng. Tuy nhiên, có thể có các tùy chọn hoặc phiên bản cao cấp với các tính năng bổ sung có thể yêu cầu trả phí.
Xoilac có hỗ trợ cho thiết bị di động không?
Xoi lac thường cung cấp ứng dụng cho các thiết bị di động như điện thoại thông minh và máy tính bảng để bạn có thể xem trực tiếp bóng đá trên các thiết bị này.
Làm thế nào để liên hệ với hỗ trợ khách hàng của Xoilac?
Thông thường, trang web hoặc ứng dụng Xoilac sẽ cung cấp thông tin liên hệ hoặc mục trợ giúp để bạn có thể liên hệ với đội ngũ hỗ trợ để giải quyết mọi vấn đề hoặc thắc mắc.
Làm thế nào để cập nhật thông tin tin tức và lịch thi đấu trên Xoilac?
Trên Xoi lac, bạn có thể thường xuyên kiểm tra mục tin tức và lịch thi đấu để cập nhật thông tin mới nhất về bóng đá, các trận đấu sắp tới, và các sự kiện khác liên quan.
Xoilac đã chứng tỏ mình là một địa chỉ tin cậy cho những người yêu thể thao và bóng đá. Với chất lượng phát sóng tốt, khả năng cập nhật lịch thi đấu đa dạng và ổn định, Xôi Lạc đã mang đến một trải nghiệm xem trực tiếp bóng đá tuyệt vời cho các khán giả. Không chỉ là một nền tảng giải trí, Xôi Lạc còn là một cổng thông tin thể thao đầy đủ và đáng tin cậy. Với đội ngũ chuyên nghiệp và cam kết không ngừng phát triển, Xôi Lạc đã và đang ghi dấu ấn mạnh mẽ trong lòng người hâm mộ.